我们知道低温的极限是约–273.15°C，也就是0 K。液氮能够帮助我们冷却到78 K（−195 °C），换用液氦则可以达到4 K（–269 °C）。传统制冷方法的极限来自稀释制冷机，最低能够达到约2mK。

追求低温的过程，是人类拓展物理学边界的过程。每当我们把温度降得更低，量子效应便会更显著，更新奇有趣的物理现象便会展现出来。比如，1911年荷兰物理学家Heike Kamerlingh Onnes将汞降低至4.2K时，汞的电阻消失了，人类第一次发现了超导现象。1937年，苏联物理学家Pyotr Kapitsa和加拿大物理学家John F. Allen & Don Misener，将氦-4降低至约2.2K时，液体的粘度变为了0。这便是著名的氦-4超流现象。

所以，2mK这个温度还远不能满足我们的好奇心，我们需要寻找实现更低温度的途径。

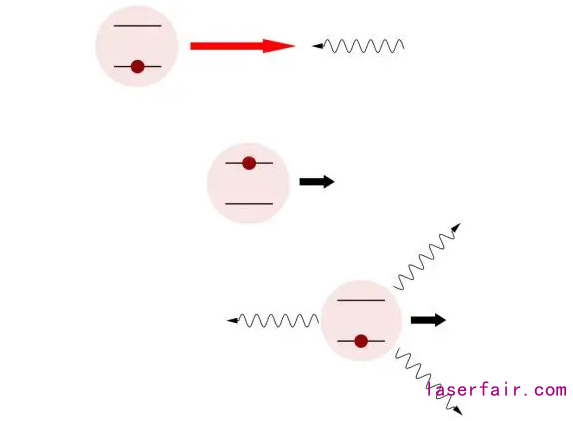
当前人类的低温记录是450 pK^[1]，也就是比绝对零度高了二十亿分之一开尔文。在此温度下原子几乎停止了运动，就像被“冻住”了一样。他们使用的核心技术便是激光冷却（图1），这是物理学家逼近绝对零度的必要手段。

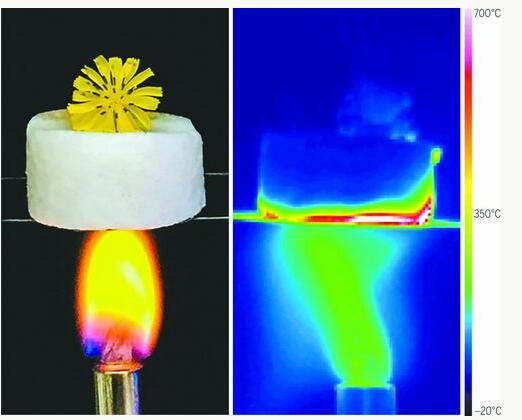
激光冷却并不是一门新的技术，早在1978年，物理学家就实现了Ba+离子的激光冷却^[2]。1997年，朱棣文因为实现了Na原子的激光冷却^[3]获得了诺贝尔物理学奖。封面图片便是一团被激光冷却的Na原子 (图中间悬浮的光点)。激光冷却技术可以说是近几十年最重要的实验技术突破，它的出现直接催生了冷原子这一门学科。

借助激光，在170nK的低温下，人类第一次制备了Rb原子的波色爱因斯坦凝聚态，所有原子同时处于同一个量子态上，量子效应得到了极致的体现。在其中光速可以被降至数米每秒。

一旦制备了超冷原子，我们便能够以前所未有的精度对其进行操控和测量。比如我们能够以万亿分之八十一的精度把精细结构常数测量到小数点后11位，α−1 = 137.035 999 206(11)^[4]，这构成了对标准模型最精密的检验。当然，最直接的应用便是原子钟，这是GPS等现代高精度系统的基石。

然而，自1978年至今的42年时间里，负离子的激光冷却从来没有被实现过。

负离子的激光冷却有两个直接的用处：研究正反物质对称性和研究超冷化学。标准模型没有告诉我们引力对于正反物质是否是等价的。为了检验这一点，物理学家选择制备低温的反氢原子，将它们在引力场中的运动与正氢原子进行比较^{[5, 6]}。制备低温反氢原子的一条路径是制备低温反质子，再往上贴附反电子。所以一旦我们实现了任何一种负离子的激光冷却，我们便可以使用协同冷却技术冷却反质子，进而制备反氢原子。同样，我们也可以使用协同冷却技术冷却任何一种我们想要的负离子，这样便可以研究极低温度下的化学反应动力学过程，加深我们对于化学反应的理解。

不过，由于缺少合适的体系，负离子激光冷却的发展受到极大制约。在过去的几十年里，负离子研究技术不断提升，从最开始的LPES^[7]，到后来的LPT^[8]、LPM ^[9]。在偌大的一张元素周期表里，物理学家却只在三个元素的负离子内部观察到了电偶极跃迁：Os– [10], La– ^[11] 和Ce– ^[12]。然而，这三种负离子都有自己本身的缺陷，要想实现它们的激光冷却不是一件容易的事情。

需要指出的是，本文提到的负离子都是指原子负离子。激光冷却负离子的另一条路径是冷却分子负离子，比如C2–，但会面临复杂的振转能级的问题。

我们课题组的工作便是找到了一个目前最适合用于实现负离子激光冷却的体系：Th–。

我们使用的方法叫做慢电子速度成像（Slow Electron Velocity–Mapping Imaging, SEVI）。我们使用一束激光脱附负离子，通过测量光子能量和脱附电子的动能研究负离子。这个方法由Neumark在2004年提出^[13]，是一种研究分子结构的新手段。我们2016年开始将它引入到原子负离子的研究当中^[14]。2018年我们搭建完成了二代低温负离子光电子能谱仪^[15]，加入了低温离子阱，所以该方法也同样适用于研究分子。

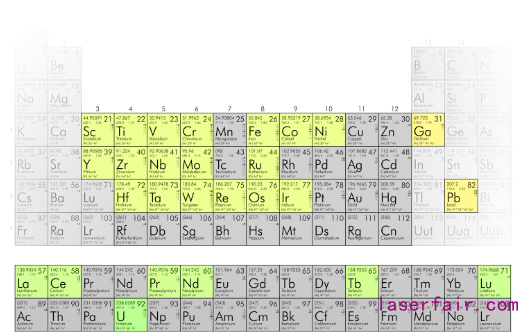
这种方法兼具超高能量分辨率与适用范围广泛的特点。光电子动能越低，它的能量分辨率越高，典型的能量分辨率为0.1 meV ^[16]。原则上，这种方法对于任何负离子体系都适用。我们使用SEVI方法，测量了大部分过渡族元素和部分镧系、锕系元素的电子亲和势 (Electron Affinity, EA) 与负离子能级结构。图2中有颜色的元素都是我们课题组测量的。我们将这些元素的电子亲和势精度提高了10 - 400倍，其中Re ^[17], Hf ^[18], U等元素的EA值是第一次在实验上被测量。过渡族元素由于其复杂的电子结构，对其进行高精度的理论计算一直是一个难点。因此，我们的实验结果可以作为很好的评判标准，指导计算方法的发展。

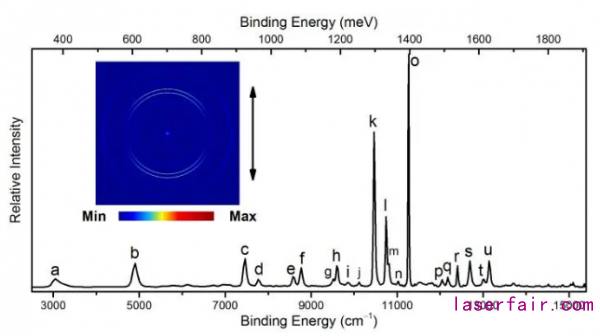
图3是我们采集到的Th–的光电子能谱^[19]。我们测定出 EA = 607.690(60) meV。这引起了我们的兴趣。前人初步的理论计算指出Th– 内存在奇偶两种宇称的能级序列^[20]，但因为计算出的EA太低，电偶极跃迁速率太慢，而把Th– 排除于激光冷却的候选体之外。我们的实验结果表明，Th–的EA值远大于之前理论计算的结果 368 meV^[20]。所以，事实上Th–是有希望可以被用于激光冷却的。

为了检验Th–的能级结构是否满足激光冷却的严苛要求，我们的合作者——复旦大学的陈重阳教授课题组进行了大规模高精度的理论计算。计算给出了Th–内奇偶宇称各个能级的位置，并且确认了存在“闭合快速的电偶极跃迁循环”，是可以用于激光冷却的。更有意思的是，考虑到232Th核自旋为0，不存在超精细结构劈裂，所以我们只需要一种波长的激光就可以实现激光冷却了，大大降低了实现难度。

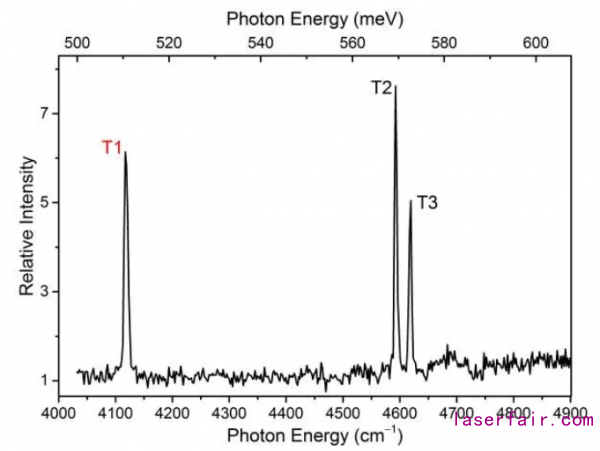
理论计算给了我们希望。我们很快改进仪器，通过双光子共振脱附的方法，在实验上第一次观测到了这个电偶极跃迁的存在（图4中T1），并且测定了其能量：123.455(30) THz^[21]。我们又通过理论计算和数值模拟确认了使用Th–协同冷却反质子是具有实用价值的。

综上所述，我们的工作表明：Th–是目前最适合实现负离子激光冷却体系，而且激光冷却技术实施技术难度较低，适用于协同冷却反质子和其他负离子。我们工作给负离子的激光冷却铺平了道路，有望促进基础物理和超冷化学等领域的发展。接下来，我们将逐步有序推进负离子激光冷却的工作。